【抽象代数】用Mathematica求代数数本原多项式

我们前面介绍了，用Mathematica可以判定代数整数和代数数的方法。那么，给定一个代数数，怎么求它的本原多项式呢？本文，我就来介绍相关命令。

东西/原料

1
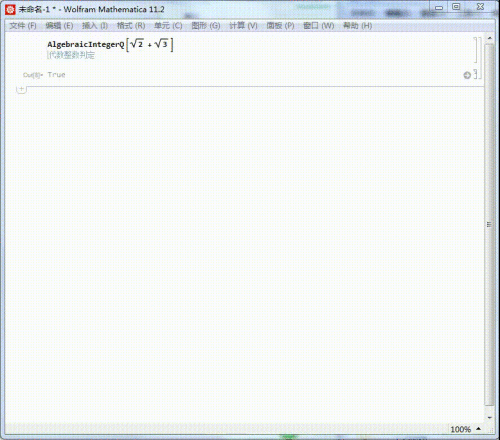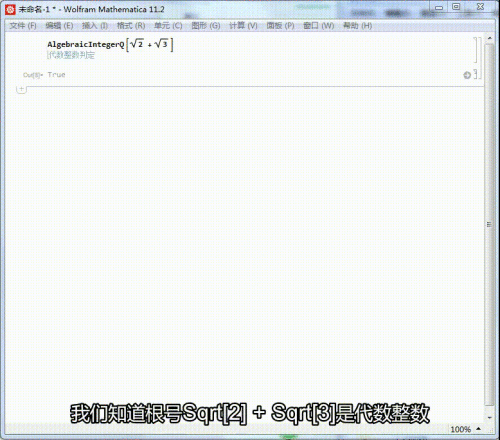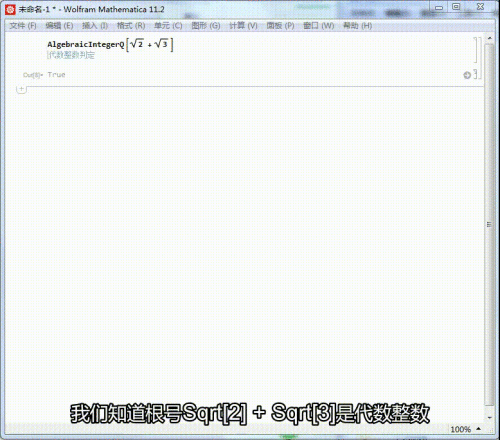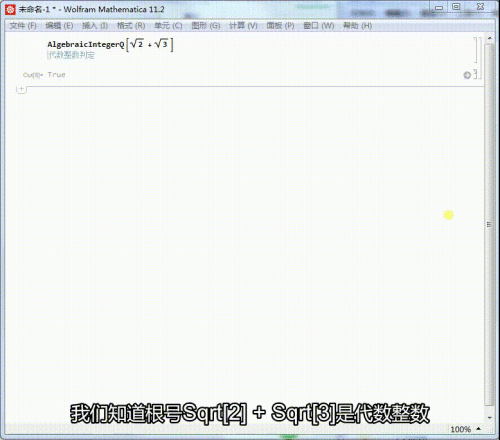
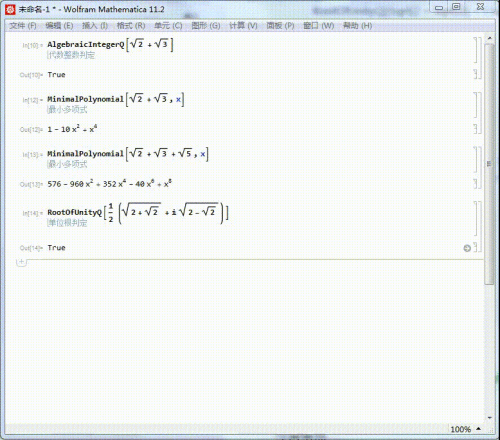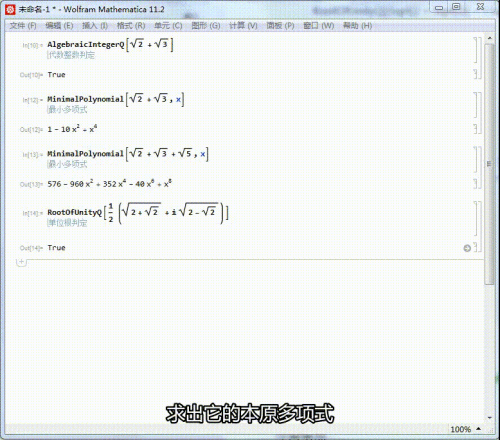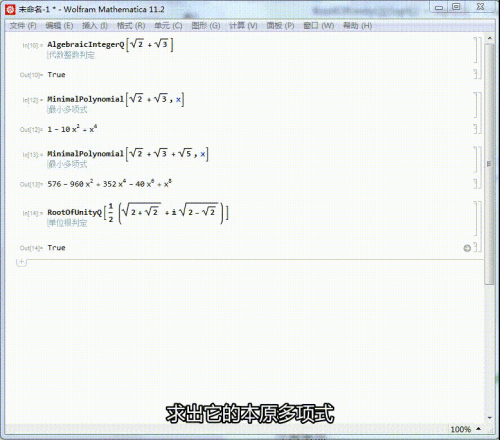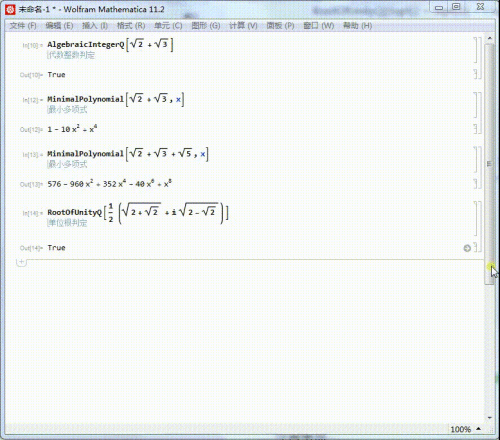
我们知道Sqrt[2] + Sqrt[3] 是代数整数，它的来源根基多项式是：
MinimalPolynomial[Sqrt[2] + Sqrt[3]]
2
上面返回的是一个纯函数。要是需要一个关于x的多项式，可以写为：
MinimalPolynomial[Sqrt[2] + Sqrt[3],x]
3
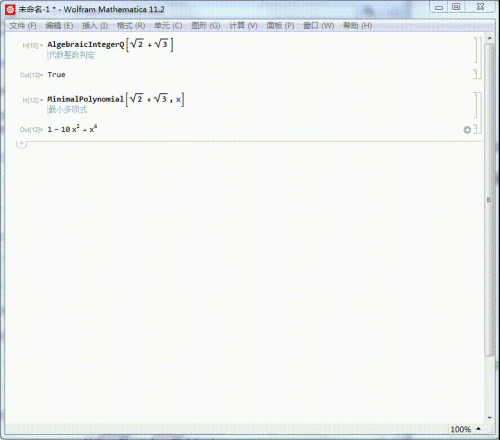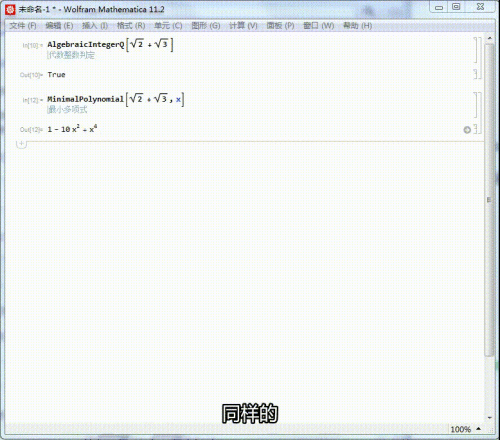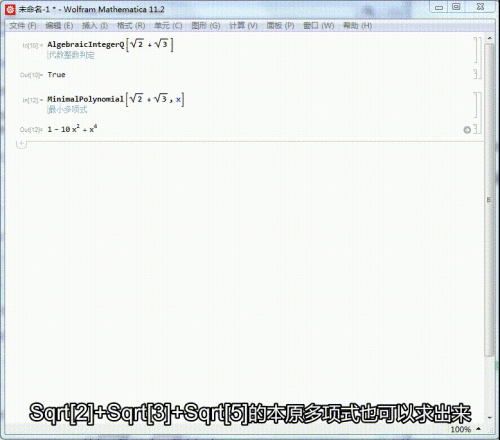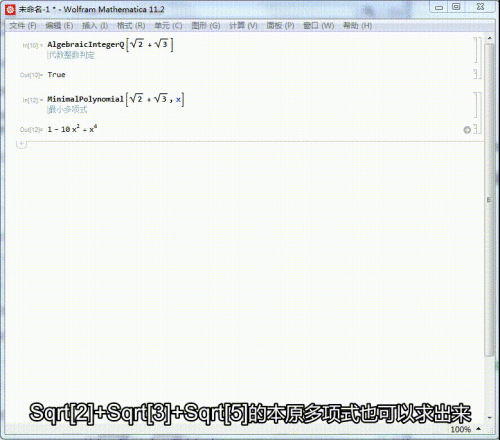
同样的，Sqrt[2] + Sqrt[3] + Sqrt[5]的来源根基多项式也可以求出来，成果获得的多项式有点庞大：
MinimalPolynomial[Sqrt[2] + Sqrt[3] + Sqrt[5],x]
4
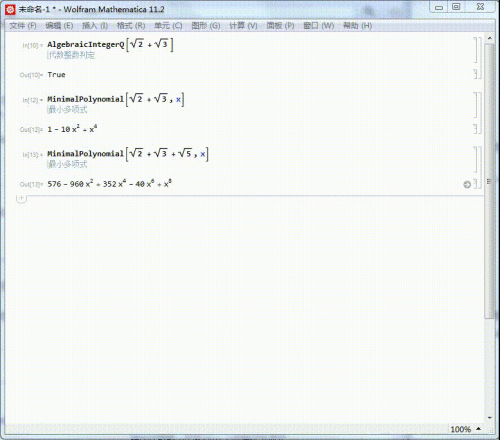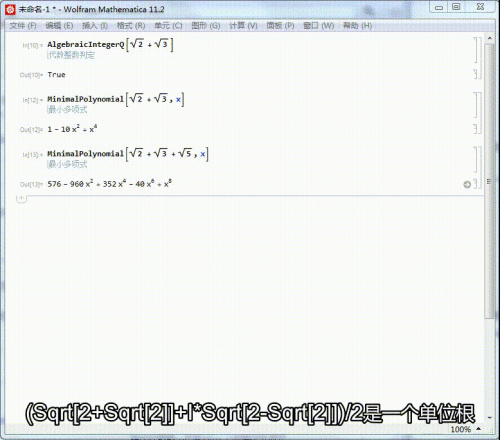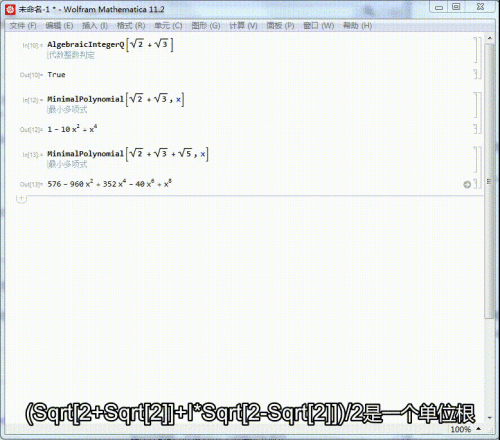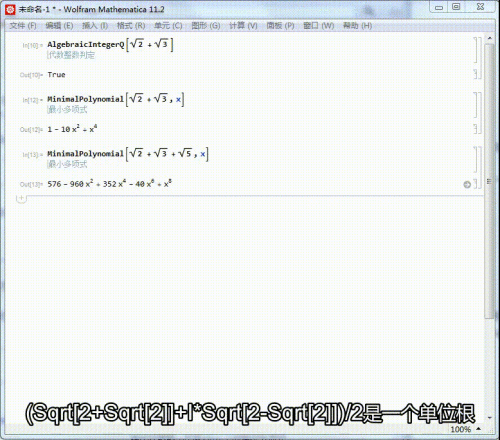
(Sqrt[2+Sqrt[2]]+I Sqrt[2-Sqrt[2]])/2是一个单元根：
RootOfUnityQ[(Sqrt[2 + Sqrt[2]] + I Sqrt[2 - Sqrt[2]])/2]
5
求出它的来源根基多项式，可以进一步证实，它是一个单元根。
它的来源根基方程是x^8+1=0，是以，它是一个16次单元根。
6
圆周率不存在来源根基多项式，以是它不是代数数。
END